It is a long-known experimental fact that hydrogen affects the mechanical properties of metals. The purpose of this study is to obtain basic knowledge about the effect of hydrogen and strain rate on the mechanical properties of aluminum alloys in micro scales by using micro-indentation. Using high-Zn Al-Zn-Mg alloys with different amounts of internal hydrogen, we compare the micromechanical characteristics with the previous theory.
The amounts of internal hydrogen for high-Zn Al-Zn-Mg base alloys were 0.12cc/100g (Low-H) and 0.33cc/100g (High-H), respectively. Table 1 shows the chemical compositions of high-H and low-H materials (mass %).
A micro-indentation using a Berkovich indenter was performed at loading rate of 70 mN/s. The indenter was loaded to a maximum value of 1200 mN, and then was maintained for 30 s.
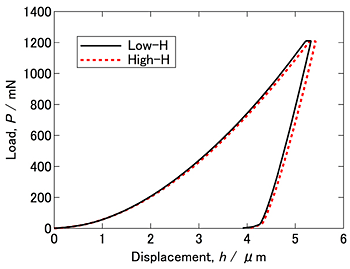
Figure 1 shows effect of internal hydrogen on load-displacement relation in the low-H and the high-H materials. The high-H material showed a tendency to decrease the load compared to the low-H material at a certain displacement. However, the amount of change is very small. Therefore, in order to evaluate this tendency in detail, the loading curvature is considered. In indentation, the loading segment of the load–displacement relation follows a parabolic trend, which is known as Kick’s law:
| P = Ch2 | (1) |
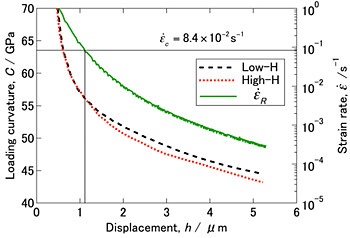
where C is the loading curvature, which is a material constant value. Figure 2 shows the relationship between typical loading curvature and displacement obtained from Eq. (1). The loading curvature at the initial stage of deformation for both the low-H and the high-H materials is almost the same. However, the loading curvature of the high-H material was lower than that of the low-H material due to a certain displacement.
In this study, we focus on changes in the strain rate of indentation. Since the indentation causes local deformation, a representative strain rate 
R has been proposed in consideration of the nonuniform field of deformation inside the specimen. The representative strain rate can be expressed by the following equation.
 |
(2) |
where 
is the displacement rate and c is the material constant. The authors have tried to determine the material constant using serration of Al-Mg alloy, and c = 0.1 was experimentally obtained. From Equations (1) and (2), the following equation can be obtained during loading control.
 |
(3) |
Figure 2 shows the relationship between R obtained from Eq. (3) and the displacement in the high-H material. The strain rate tended to decrease continuously from 100 s-1 to 10-4 s-1 with increasing displacement. On the other hand, the limit strain rate affected by hydrogen is given by the following equation.
| c = ρbvc |
(4) |
where, vc is the limit value of the dislocation rate at which hydrogen can move while adhering to the dislocation, and ρ is the dislocation density. If the dislocation density is 1010 m-2 and is substituted into the above equation, the limit value of the strain rate at which the dislocation can transport hydrogen is = 8.4 
10-2 s-1. The results are shown in Fig. 2. Looking at the amount of displacement at the intersection of the representative strain rate and the limit strain rate, the displacement was almost consistent with the difference in loading curvature between the low-H and high-H materials.
