High-temperature Creep Mechanism of Dual Ductile-phaseMagnesium Alloy with Long-period Stacking Ordered Phase

Masami Fujiwara¹, Hidenari Takagi¹, and Kenji Higashida²

¹ Division of Applied Physics, Department of General Education, College of Engineering,
Nihon University, Koriyama 963-8642, Japan.
² Department of Materials Science and Engineering, Faculty of Engineering,
Kyushu University, Fukuoka 819-0395, Japan.

Our team has been reporting the interpretation of the high-temperature creep mechanism for dual ductile-phase alloy by theoretical analyses, indentation creep tests, and finite-element simulations. The experimental results suggested that the creep strength of the dual ductile-phase alloy closely followed the rule of mixtures and the isostrain rate conditions. The stress exponent n for creep was expressed by the harmonic mean weighted by the effective volume fractions of the constituent phases, which strongly depended on the deformation rate. In addition, n consistently fell between the corresponding values for the two constituent phases in the power-law creep region. A similar trend was observed for the deformation rate dependence of the creep activation energy Q, which was expressed by the weighted arithmetic mean value. Thus, the values of n and Q quantitatively captured the mechanical contribution of the reinforcing phase to the creep strength of the overall dual ductile-phase alloy. As following, the microstructure of the tested alloy and experimental results of the stress exponent are shown.

Figure 1 shows a representative SEM image of the three-dimensional microstructure of the dual-phase alloy. In the longitudinal section parallel to the extrusion direction (ED), the discontinuous fibrous LPSO phase (light gray) is aligned with the ED in the α-Mg matrix (dark gray). Meanwhile, in the cross-section perpendicular to the ED, the lamellar LPSO phase is uniformly observed in the α-Mg matrix. The area fraction of the α-Mg matrix is ~75% for all cross-sections (i.e., a volume fraction of V₁0.75 for the matrix and V₂0.25 for the remaining LPSO phase). The values of V₁ and V₂ are unchanged after heat treatment.

Figure 2 shows the IPF map of the longitudinal section immediately under the indentation mark. In this case, indentation was performed with a conical indenter perpendicular to the cross-section at the highest test temperature of 673 K for a loading time of 5.4 ks. During this loading period, neither recrystallization nor microscopic cracking occurs in the region. These findings show that the indentation creep test is performed on a thermally stable microstructure. Although a small amount of as-worked α-Mg grains exist in the microstructure, it is thought that they have little influence on the cross-sectional indentation test results.

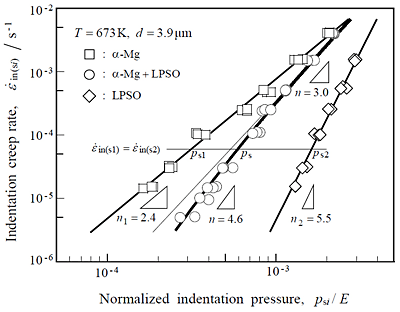
Figure 3 shows double logarithmic plots of ε ’_in(si) versus p_si/E for the α-Mg alloy, the LPSO alloy, and the dual-phase alloy. Here, p_s1 of the α-Mg alloy is the lowest, p_s2 of the LPSO alloy is the highest, and p_s of the dual-phase alloy is consistently located between them. In the case of single phase alloy of α-Mg or LPSO alloy, the data points follow different straight lines. The gradient line for α-Mg alloy corresponds to n₁ = 2.4, and it for LPSO alloy is n₂ = 5.5. In contrast, The data points for the dual-phase alloy follow a continuous curve, when ε ’_in(si) decreases from 4.5 10^-3 s^-1 to 1.0 10^-4 s^-1, n increases from 3.0 to 4.5. The n value of dual-phase alloy gradually approach the corresponding value of the LPSO phase (n₂ = 5.5) as the deformation rate decreases. These findings indicate that the characteristic creep parameters of dual-phase alloy cannot be explained using the traditional creep theory for single-phase alloys.

Additional results in this paper are as follows:

•
During the creep of the LPSO phase, the basal <a> slip system was dominant. However, the steady-state creep behaviors of the LPSO phase could not be explained using the conventional creep theory for single-phase alloys. Meanwhile, GBS occurred in the fine-grained α-Mg matrix, so that the strain component in the c-axis direction of the α-Mg grains could be compensated for maintaining the ductility.

•
The creep characteristic values n and Q of the dual-phase alloy strongly depended on the deformation rates, which were intermediate between the corresponding values of the two constituent phases in the power-law creep region. The magnitude of the load shared by the LPSO phase varied following the effective volume fraction in the mixing rule and as a function of the deformation rate.

•
The values of n and Q were theoretically predicted using the creep properties of single-phase alloys with the same composition as the constituent phases. The mechanical contribution of the LPSO phase to the creep strength of the overall dual-phase alloy could be estimated from the creep characteristic values of the alloy.

•
In the power-law creep region, the LPSO phase effectively suppressed deformation of the α-Mg matrix by composite reinforcement, thereby achieving high creep strength. In addition, the bridging phenomenon occurred in the dual-phase alloy, yielding a high reinforcement efficiency.

•
To further improve the creep strength of the dual-phase alloy, it is effective to increase the toughness and reinforcement efficiency of the LPSO phase. It is important to develop a method for elucidating the high-temperature creep mechanism of such an alloy, thereby reducing the development times of new materials with complicated structures.

[Published in Materials Transactions, 60 (2019) 503-512]


Fig. 1 An SEM image of the three-dimensional microstructure of the dual-phase extruded Mg alloy. The LPSO phase (light gray stripes) is aligned along the extrusion direction, ED, in the α-Mg matrix (dark gray).


Fig. 2 Crystal direction map of the longitudinal section immediately under the indentation mark.


Fig. 3 Double logarithmic plots of the experimental creep data for the α-Mg alloy, LPSO alloy, and their dual-phase alloy. The data points for the dual-phase alloy follow the thick curve, which is obtained by applying the rule of mixtures and the isostrain rate condition to the straight lines.

•	During the creep of the LPSO phase, the basal <a> slip system was dominant. However, the steady-state creep behaviors of the LPSO phase could not be explained using the conventional creep theory for single-phase alloys. Meanwhile, GBS occurred in the fine-grained α-Mg matrix, so that the strain component in the c-axis direction of the α-Mg grains could be compensated for maintaining the ductility.
•	The creep characteristic values n and Q of the dual-phase alloy strongly depended on the deformation rates, which were intermediate between the corresponding values of the two constituent phases in the power-law creep region. The magnitude of the load shared by the LPSO phase varied following the effective volume fraction in the mixing rule and as a function of the deformation rate.
•	The values of n and Q were theoretically predicted using the creep properties of single-phase alloys with the same composition as the constituent phases. The mechanical contribution of the LPSO phase to the creep strength of the overall dual-phase alloy could be estimated from the creep characteristic values of the alloy.
•	In the power-law creep region, the LPSO phase effectively suppressed deformation of the α-Mg matrix by composite reinforcement, thereby achieving high creep strength. In addition, the bridging phenomenon occurred in the dual-phase alloy, yielding a high reinforcement efficiency.
•	To further improve the creep strength of the dual-phase alloy, it is effective to increase the toughness and reinforcement efficiency of the LPSO phase. It is important to develop a method for elucidating the high-temperature creep mechanism of such an alloy, thereby reducing the development times of new materials with complicated structures.