The mechanical properties of metallic materials can be controlled by both metallurgical methods and structural design. In the latter, introduction of pores can effectively reduce Young's modulus. The porous structure can not only imitate structure and mechanical properties of living bone, but also facilitate bone ingrowth into the porous structure. Therefore such porous implants have long been sought as the ideal bone substitute. For example, porous Ti compacts have been fabricated by controlling by powder size and sintering conditions. It was shown that the Young's modulus and the proof and bend stresses are inversely proportional to the porosity; the fabricated compacts with a porosity of approximately 30 vol% showed mechanical properties equivalent to those of human cortical bone. In another previous study, porous Ti was fabricated by the space holder method, which is a very simple method of preparing porous devices with random pores. Above 60% of porosity, all pores were connected.
Recently, great advancements have been made in additive manufacturing (AM) technology, also commonly known as three-dimensional (3D) printing. Powder bed fusion is a common technology used in 3D printing, particularly when applied to metallic materials. This layer-by-layer fabrication technique is well suited to the design and production of tailor-made metallic products with complex shapes, including porous materials, especially for medical applications such as artificial bone and replacement joints. In the future, such applications will undoubtedly expand rapidly; however, it will necessitate to develop AM techniques for modelling fine structures with sub-millimetre scale in order to give further advanced functions.
The aim of this study was to fabricate a small porous structure composed of units with sub-millimetre dimensions from pure Ti powder by AM. The target device has a simple structure that makes it easy to fabricate using conventional AM techniques. Additionally, the mechanical properties of porous Ti were investigated.
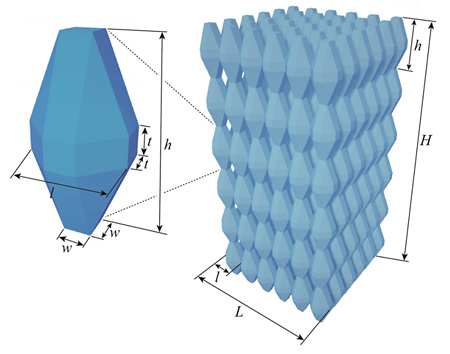
Rhombicuboctahedron-derived units were used to design the structure, as shown in Fig. 1, and the entire porous structure consisted of 216 units (6 
6 6 in the width, in-plane depth, and height directions). This structure can be easily manufactured in any direction because it does not have orthogonal planes. Five types of porous Ti samples and one dense Ti sample were fabricated with the laser AM machine (EOSINT M 270, EOS, Germany). The appearances of the samples were observed using a digital camera (Stylus TG-4 Tough, Olympus) and are shown in Fig. 2. The fabricated porous structures appear as designed, though the flat planes in the rhombicuboctahedron-derived unit structure could not be precisely reproduced as a result of surface tension during melting. In addition, the region where the connection faces of the unit structures are joined (connection regions) have a cylindrical shape in the porous Ti samples with w/l = 0.30 and 0.35. No significant visible distortion was observed in any of the samples on the whole.
A compressive test was performed to compare the mechanical properties of the structures with different unit dimensions. All stress–strain curves were typical and smooth, as in ductile bulk metals. The gradients of the curves in elastic region and the proof stresses were obtained from the stress–strain curves.
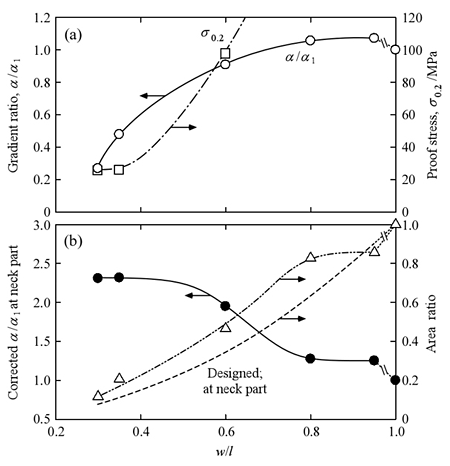
The gradient ratios α/α1 and proof stresses σ0.2 obtained from the stress–strain curves for the porous Ti samples are plotted against w/l in Fig. 3(a). The gradient ratio increased with increasing w/l, saturated above w/l = 0.8, and decreased slightly in the dense sample prepared as a rectangular parallelepiped. The yield stress increased drastically with increasing w/l. The yield stress could not be measured in the porous Ti samples with w/l = 0.8 and 0.95 and the dense sample because of the limitations of the equipment. The ratio of the minimum cross-sectional area to the nominal cross sectional area of the porous Ti samples in the plane perpendicular to the load axis and the corrected gradient ratio calculated from this area ratio are also plotted against w/l in Fig. 3(b). The corresponding designed area ratio is also plotted as a broken line. The measured area ratios were slightly larger than the designed area ratios, but both showed the same trend, as mentioned above. The corrected gradient ratio was then re-calculated under the assumption that the load was borne exclusively by the regions of minimal cross-sectional area (Fig. 3(b)). In the porous Ti samples with w/l ≥ 0.80, the corrected gradient ratio was approximately 1.2, which is almost equivalent to that in the dense Ti. In contrast, in the samples with greater porosity, the corrected gradient ratio was larger, reaching approximately 2.3 at w/l = 0.30 and 0.35. The value was almost twice that of the dense one in spite of similar solidified titanium in both samples. This indicates that the neck parts with small w/l may have solidified after completely melting. In the portion except for the necks, it implies that the local Young's modulus in the AM samples did not reach that of melted pure Ti ingot. Furthermore, the microstructure including a texture might be important to understand this phenomenon clearly. Further experiments would be required in order to clarify the effect of microstructure on the mechanical properties in the AM titanium.
