Phonon scattering at the interfaces of epitaxially grown
Fe2VAl/W and Fe2VAl/Mo superlattices

Satoshi Hiroi1,2, Shunsuke Nishino2, Seongho Choi2, Okkyun Seo1, Jaemyung Kim1, Yanna Chen1,
Chulho Song1, Akhil Tayal1, Osami Sakata1, and Tsunehiro Takeuchi2,3
1Synchrotron X-ray Group, Research Center for Advanced Measurement and Characterization,
National Institute for Materials Science (NIMS), Kouto, Sayo 679-5148, Japan
2Research Center for Smart Energy Technology, Toyota Technological Institute, Nagoya 468-8511, Japan
3CREST, Japan Science and Technology Agency, Toyota Technological Institute, Tokyo 102-0076, Japan

We investigated the cross-plane thermal conductivity and boundary thermal resistance of epitaxially grown superlattice samples. These included iron vanadium aluminum alloy (Fe2VAl) and tungsten (W) or molybdenum (Mo) prepared by radio frequency magnetron sputtering.

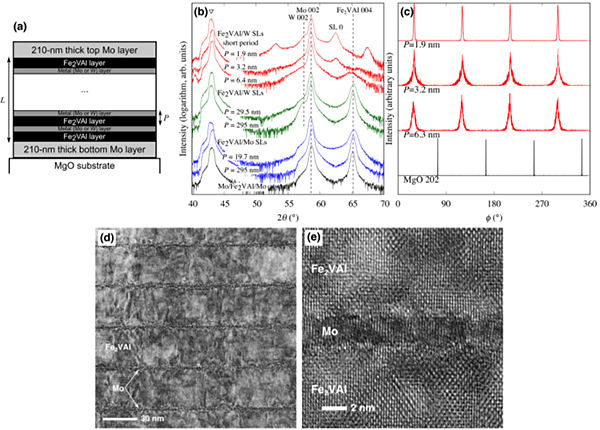
Fe2VAl/W and Fe2VAl/Mo superlattice samples were deposited on the (100) surface of MgO single crystal substrate by radio frequency magnetron sputtering. W and Mo metals are appropriate materials to construct the epitaxially grown Fe2VAl-based superlattice because they have bcc lattice structure and provide with a smooth-surface layer by the sputtering technique. We also deposited a 210-nm-thick Mo layer at the bottom and top surfaces of the superlattice to enable accurate measurements of the thermal diffusivity by a time-domain thermoreflectance (TDTR) method with a rear-heating front-detection (RF) configuration. A schematic drawing of the Fe2VAl/metal superlattice is also shown in Fig. 1(a).

The symmetric θ–2θ X-ray diffraction patterns acquired for the Fe2VAl/W and Fe2VAl/Mo superlattices are shown in Fig. 2(b). In a sample having a period of more than 20 nm, we clearly observed the 004-diffraction peak of the Fe2VAl Heusler phase as previously reported for three layered epitaxially grown films. The 004 peak was less intense in the sample with a period less than 6.4 nm, presumably because of distortion or dislocations. In the sample with the shortest period of approximately 1.9 nm, a sharp Fe2VAl 004 peak with satellite peaks was clearly observed owing to the formation of a well-ordered superlattice. This lattice was clearly expanded/contracted by the 10 % mismatch of the lattice constants between W and Fe2VAl. In thin layers, the stress must be homogeneous to realize well-ordered structures. Notably, the lattice constant value of 0.5953 nm, as calculated from the zero-order superlattice reflection at 2θ = 62.4°, corresponds to the average value of the lattice constants of bulk Fe2VAl and W. The azimuthal scan around the Fe2VAl 202 peaks shown in Fig. 1(c) indicated fourfold symmetry. These peaks were located at a 45° angle from the fourfold peaks of MgO 202. In the sample with the thinnest period, we observed very sharp fourfold peaks around the zero-order superlattice reflection. This result provides further evidence for the highly ordered superlattice structure in the sample at short period lengths. The broadening of the peaks became most pronounced for a period of 3.2 nm. At this critical period, dislocations formed, which together with critical stress contributed to a highly disordered structure.

The periodic length dependence of the thermal conductivity of the superlattice at room temperature is shown in Fig. 3(d). The thermal conductivity in superlattices with a long period exceeding 100 nm remained constant. Conversely, we observed a steady decrease of the thermal conductivity with a decreasing period less than 100 nm. This property reached 3.4 W m-1 K-1 at the shortest period of 1.9 nm, and this value is 55 % smaller than that observed for samples exceeding 100 nm. The existence of a minimum thermal conductivity has been reported for various superlattice samples and is generally attributed to the coherent-incoherent crossover of phonons. Our current samples did not show a minimum in the periodic length dependence of thermal conductivity, which has been commonly reported previously. Here, the large lattice mismatch and misfit dislocation in the metal layer is likely related to the coherent-incoherent crossover of phonon modes involving thermal transport. Imperfect connections of crystal lattices, for example, elemental mixing, interface roughness, and dislocations, disrupt the coherency of phonon modes at the interlayer boundaries. These effects might explain why the crossover was not observed in the superlattices prepared in this study because short-wavelength phonons are supposed to be scattered by defects. The increase of the thermal conductivity over the extremely thin period region of the superlattice was weakened, i.e. boundary phonon scattering decreased with decreasing period.

We found the same trend in the thermal conductivity of the Fe2VAl/Mo superlattice. However, the thermal conductivity in the period range below 100 nm was slightly higher than that of the Fe2VAl/W superlattice. Differences of the thermal conductivity of the two metallic layers should not be related to the measured thermal conductivity because the volume fractions of W and Mo layers make up only 3.3 % of the superlattices. Hence, boundary thermal resistance strongly depends on the component materials. We quantitatively calculated the boundary thermal resistance, R, at the interface between Fe2VAl and W or Mo layers. We successfully obtained good results for periods greater than 20 nm, shown as solid curves in Fig. 3(d).

The boundary thermal resistance in the thicker period region indicated different constant values for the Fe2VAl/W and Fe2VAl/Mo superlattices. Both W and Mo having bcc lattices had almost the same lattice constant; therefore, the mass difference of those elements determined the thermal resistance. This result is consistent with molecular dynamics simulations. Hence, the higher boundary thermal resistance for the Fe2VAl/W superlattice is attributed to greater mismatch of the phonon densities of states between their layers, particularly in the long wavelength region.

In conclusion, we investigated the cross-plane thermal conductivity and boundary thermal resistance of epitaxially grown superlattice samples. These included iron vanadium aluminum alloy (Fe2VAl) and tungsten (W) or molybdenum (Mo) prepared by radio frequency magnetron sputtering. We used out-of-plane X-ray diffraction measurements to confirm the epitaxial growth of the superlattices. The superlattice with the shortest period of 1.9 nm showed satellite reflections indicating a highly ordered structure. Misfit dislocations in the 2-nm-thick Mo layer were also identified by high-resolution transmission electron microscopy. We attribute these features to the large lattice mismatch between the Fe2VAl and Mo lattices. The cross-plane thermal conductivity of the superlattice decreased as the number of interfaces increased because of thermal resistance at inter-layer boundaries. A simulation of the thermal conductivity by the constant boundary resistance model reproduced the experimental data but with some deviations for samples with a smaller period (less than 20 nm). This deviation from the simulation results indicates that the phonon modes contributing to the thermal transport changed and/or the phonon scattering probability at the interfaces decreased. The superlattice of Fe2VAl/W with a period thickness greater than 20 nm had a boundary thermal resistance approximately twice as large as that of the Fe2VAl/ Mo superlattice. This result provides clear evidence for the effects of the mass difference of layers on phonon scattering at an interface.

[Published in Journal of Applied Physics 125, 225101 (2019). doi:10.1063/1.5080976]

Fig. 1 (a) A schematic of the superlattice structure. (b) Symmetric θ–2θ X-ray diffraction patterns of Fe2VAl/metal superlattices with varying period thickness. SL 0 is the zero-order satellite reflection and the triangle marker indicate the contribution of the MgO substrate. (c) Azimuthal scans around Fe2Al 202 peak, MgO 202 peak, and zero-order satellite reflection near Fe2VAl 202 peak for Fe2VAl/W superlattices. (d) and (e) Cross-sectional transmission electron microscope images of a Fe2VAl/Mo super- lattice having a 40-nm period.
Fig. 2 Reciprocal space map around W 202, Mo 202, and Fe2VAl 404 reflection for Fe2VAl/W superlattices having period thicknesses of (a) 1.9 nm, (b) 3.2 nm, and (c) 6.4 nm. Black lines indicate relaxation of the cubic lattice. Points on the relaxation line indicate predicted Bragg reflections for the W 202, Mo 202, and Fe2VAl 404 planes of the bulk materials.
Fig. 3 Results of TDTR measurements of the superlattices. Transient temperature curves of (a) Fe2VAl/Mo and (b) Fe2VAl/W superlattices with fitting results according to Eq. (1) shown by black curves. (c) The definition of the areal heat diffusion time drawn as a shaded area. The solid and broken curves correspond to the transient curve of adiabatic and nonadiabatic condition, respectively. (d) Period dependence of the cross-plane thermal conductivity for superlattices obtained by the areal heat diffusion time method. Solid curves indicate the best fitting results calculated from Eq. (6) for Fe2VAl/Mo (blue) and Fe2VAl/W (red) superlattices. (e) Thermal resistance, L/κSL in the superlattice as a function of number of metal layers, n. The open triangle and circle indicate the expected thermal resistance without the boundary thermal resistance for the W-contained superlattices with total thicknesses of 290 and 195 nm, respectively. The solid lines are calculated thermal resistances by Eq. (6) with fitted κFVA and R. The dashed lines correspond to the expected thermal resistance for the W-contained superlattices with constant boundary thermal resistance obtained by the superlattice with 590 nm in total thickness. (f) Period dependence of the boundary thermal resistance of Fe2VAl/metal interfaces. Solid lines indicate the boundary thermal resistances (BTR) of Fe2VAl/Mo (blue) and Fe2VAl/W (red) interfaces.