It is widely accepted that creep behavior are mainly evaluated by minimum or steady-state creep rate. The major important parameters are its stress dependence and temperature dependence. Binary solid solution alloys such as aluminum-magnesium alloy is typical alloy that its strain rate can be organized by a power law. One of the general forms of equations that describe steady-state or minimum creep rate is the equation proposed by Mukherjee, et al. [1], and the equation can be shown as Eq. (1) when the activation energy of creep is not significantly different from the activation energy for diffusion.
| (1) |
Here, A', D, N and m are a constant to be determined experimentally, the diffusion coefficient, the solute concentration and the concentration constant, respectively. In this case, creep behavior is characterized by the solute concentration, m, and the stress exponent, n. In power law creep of the solid solution alloys, it is well known that Alloy-type behavior of the stress exponent about 3, and Metal-type behavior of stress exponent about 5 appear depending deformation condition and concentration[2-3]. This creep behavior is intended to be organized focusing on the steady-state or minimum creep rates, so the creep rate should be evaluated as accurate as possible. The minimum strain rate, however, could not be observed when the transient creep takes long time, or wrong creep rate could be evaluated by apparent steady-state. One should pay attention not only to the minimum creep rate but also to the shape of creep curve in transient stage for detailed analysis of creep behavior. Authors have focused on strain rate change during creep as an evaluation index of creep behavior, and have proposed a way to extrapolate creep curve from a part of creep curve [4-5]. In this paper, we evaluate the transition creep curve of aluminum-magnesium solid solution alloy quantitatively, and extrapolate the whole creep curve based on the concept of Strain Acceleration and Transition Objective index (SATO-index) including imaginary minimum strain rate.
The characteristic value, strain-acceleration- parameter (SATO-index), α, is defined as follows:| (2) |
The value, α, corresponds to the curvature of the common logarithm of strain rate as a function of strain. The value is defined at a strain of minimum creep rate, ![]() min , and the time at minimum creep rate tmin. Based on the definition of the value, the creep curve can be extrapolated and reconstructed with suitable initial conditions. The common logarithm of creep rate, log
min , and the time at minimum creep rate tmin. Based on the definition of the value, the creep curve can be extrapolated and reconstructed with suitable initial conditions. The common logarithm of creep rate, log ![]() , as a function of strain,
, as a function of strain, ![]() , gives a differential equation which explains strain and time relations, i.e. creep curve. When strain-rate can be represented by the differential equation, the minimum creep rate
, gives a differential equation which explains strain and time relations, i.e. creep curve. When strain-rate can be represented by the differential equation, the minimum creep rate ![]() min will be extrapolated from part of creep curve, even when the minimum strain rate is not explicitly observed. Here, the extrapolated minimum creep rate is defined as "imaginary minimum strain rate (imaginary
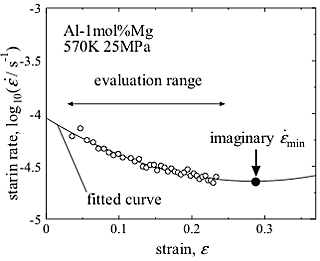
min will be extrapolated from part of creep curve, even when the minimum strain rate is not explicitly observed. Here, the extrapolated minimum creep rate is defined as "imaginary minimum strain rate (imaginary ![]() min ) ". Fig. 1 shows an example of diagram of the strain range used in the evaluation of SATO-index, and the imaginary minimum strain rate represents the value at the vertices of the approximate curve given by the differential equation. Creep curves subjected to current analysis are creep curves obtained by constant stress creep tests of Al-1mol%Mg solid solution alloy in air at 4
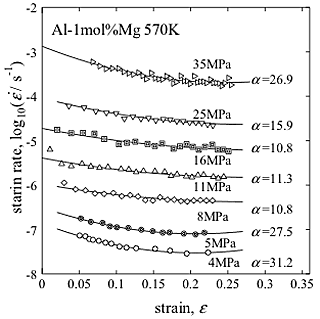
min ) ". Fig. 1 shows an example of diagram of the strain range used in the evaluation of SATO-index, and the imaginary minimum strain rate represents the value at the vertices of the approximate curve given by the differential equation. Creep curves subjected to current analysis are creep curves obtained by constant stress creep tests of Al-1mol%Mg solid solution alloy in air at 4![]() 35MPa at 570K [3,6]. Evaluation range used for SATO-index, α, is in the strain and time range of transient creep. Fig. 2 shows the relationship between strain rate and strain obtained by experiments in Al-1mol%Mg solid solution alloy at 570K. Evaluated values of SATO-index, α, are also shown on the figure.
35MPa at 570K [3,6]. Evaluation range used for SATO-index, α, is in the strain and time range of transient creep. Fig. 2 shows the relationship between strain rate and strain obtained by experiments in Al-1mol%Mg solid solution alloy at 570K. Evaluated values of SATO-index, α, are also shown on the figure.
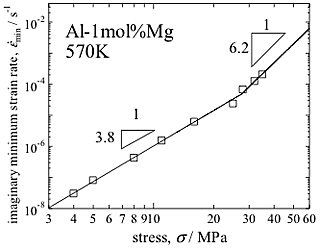
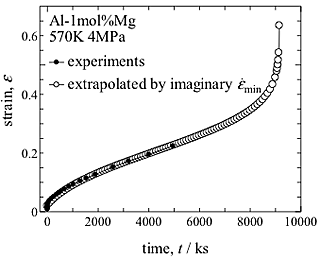
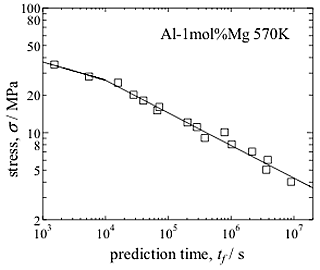
Fig. 3 shows the stress dependence of the imaginary minimum creep rate as a function of the applied stress. The stress exponent changes from 3.2 to 6.2 at about 25MPa. The transition is similar to that of deformation mechanism from Alloy-type to Metal-type [2-3]. Fig. 4 shows an example of extrapolation and reconstruction of entire creep curve obtained by numerical integration of differential equation. The extrapolated creep curve agrees well with the experiment. Even when the minimum creep rate is not observed experimentally, the extrapolated creep curves agree well with experiment. This result suggests that creep behavior of solid solution alloys can be predicted to some extent from the short creep test. Fig. 5 shows stress dependence of predicted time to failure. Predicted time to failure has a power-law relationship when the time to failure is evaluated from transient creep by SATO-index, and shows the transient in slope at 25MPa.
In present investigation, it is confirmed that it is possible to extrapolate and reconstruct a creep curve from transient creep in aluminum-magnesium solid solution without explicit appearance of the minimum creep rate. Imaginary minimum creep rate can be extrapolated by evaluating SATO-index. The value of SATO-index, α, is lower in the stress range from 9 to 15MPa. The stress range corresponds to the range where the Alloy-type behavior appears at the temperature [2,3]. The value increases both in the high stress and low stress regions, where the Metal-type behavior appears. SATO-index reflects stability of strain rate during creep and shows transient creep appears significantly in Metal-type creep conditions. The stress exponent increases from 3.8 to 6.2 at about 25MPa and the stress is roughly agree with that of the transient stress from Alloy-type to Metal-type creep. It is considered that the shape of the creep curve depends on deformation mechanisms. Not only the steady state or minimum creep rate, creep behavior in transition creep changes depending on deformation mechanisms. As for the prediction of creep life by extrapolated creep curve, power-law relations between time to failure and the applied stress are obtained in wide stress ranges. This relationship appears in the magnesium-aluminum solid solution alloy as well, and time to failure is predictable. It can be said that time to failure can be predicted from a part of creep curve in some solid solutions.
[1] A.K. Mukherjee, et al.: The Interaction between Dislocations and Point Defects, Vol. II, Part III, ed. by B.L. Eyre, Atomic Energy Authority, Harwell, UK, (1968), 422-495.
[2] H. Oikawa, H. Sato and K. Maruyama, Materials Science and Engineering, 75(1985), 21-28.
[3] H. Sato and H. Oikawa, Scripta Metall., 22(1988), 87-92.
[4] H. Sato, K. Fujita: Keikinzoku, JILM, 60 (2010), 353-5.
[5] H. Sato, T. Miyano: ICSMA-15 Journal of Physics: Conference Series 240 (2010) 012089
[6] H. Sato: Suppl.Proc, Vol.3, 137th Annual Meeting & Exhibition, TMS2008, (2008), 199-204.
[7] Hiroyuki Sato et al., Key Engineering Materials, 592-593(2013), 606-609.