Changes in the lattice constants of 55 Al-based solid solutions, as well as local lattice distortions induced by solute atoms, were studied on the basis of first-principles calculations using 3.70, 3.13, 1.56, and 0.93 at.% alloys. In all 55 theoretical Al-X systems, a linear relationship between the atomic volume and solute concentration was confirmed in the concentration range less than 3.70 at.%. Thus, the volume size factors can be calculated from these linear relationships. In all 55 theoretical Al-X systems, fairly constant values were obtained for the interatomic distances between the first nearest-neighbor solute and solvent Al atoms. Thus, the misfit strains are based on the average values of the first nearest-neighbor interatomic distances in Al26X1, Al31X1, Al63X1, and Al107X1. The misfit strains at the first nearest-neighbor sites are interaction free in the concentration range less than 3.70 at.%. However, the misfit strain at more distant neighbor atoms is much more complex than that at the first nearest neighbor. The misfit strain at the second nearest neighbor is evidently affected by the supercell size.
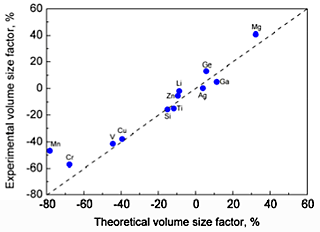
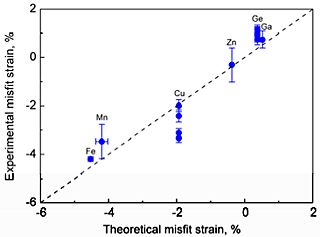
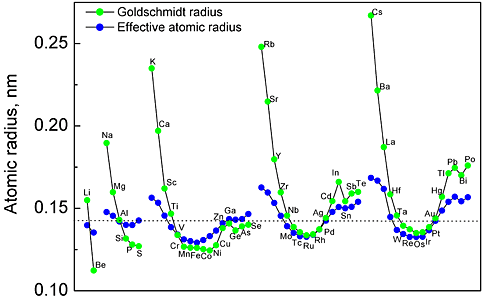
A comparison of the volume size factors calculated from the first principles with the available experimental data is shown in Fig. 1. The experimental values of the misfit strains are compared with the values from the present first-principles calculations in Fig. 2 The calculated volume size factor and the misfit strain are in good agreement with the available experimental data in the literature. The misfit strain increases linearly as the volume size factor increases. This linear relation is explained by using the Eshelby approach. Apparently, the simple Eshelby approach may provide a reasonable estimate of the misfit strain. The effective atomic radius was determined by using the hard sphere approximation. Figure 3 shows the calculated effective atomic radius based on the first principles for all 55 Al-X solid solutions considered in this study along with the Goldschmidt radius. The effective atomic radius is generally different from the Goldschmidt radius in magnitude and even in sign in some cases.
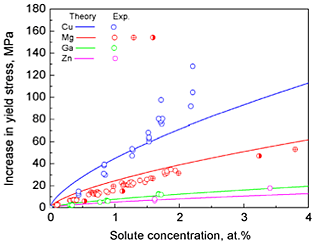
A discussion of the application of the misfit strains to the estimation of increasing yield stress due to the solid solution strengthening was presented. The dependence of the contribution to the yield stress due to the solid solution strengthening on the solute content is shown in Fig. 4. The room temperature experimental results for Al-Mg, Al-Zn, Al-Ga, and Al-Cu alloys are also shown in this figure. The calculated extent of solid solution strengthening was in good agreement with the available experimental values. In equilibrium processing, the most effective additional elements for the solid solution strengthening are predicted to be Mg, followed by Mn, Zn, and Cu. This is consistent with the experimental results, showing that Mg and Mn are major additional elements used to achieve solid solution strengthening in commercial aluminum alloys. The calculated misfit strain data can be employed to predict the solid solution strengthening of Al-based solid solutions, and thus, can potentially be used as a guide for the development of Al alloys that exhibit very high yield strength, including supersaturated solid solutions derived from non-equilibrium processing.