Improvement in rectification ratio of an Al-based bulk thermal rectifier working at high temperatures

In this study, we attempted to improve the thermal rectification ratio (TRR = (J_AB J_BA)/J_BA) of a thermal rectifier consisting of two Al-based alloys, Al_72.6Re_17.4Si₁₀ and Al_71.6Mn_17.4Si₁₁, both of which are known to be the 1/1-cubic approximant of icosahedral quasicrystal.

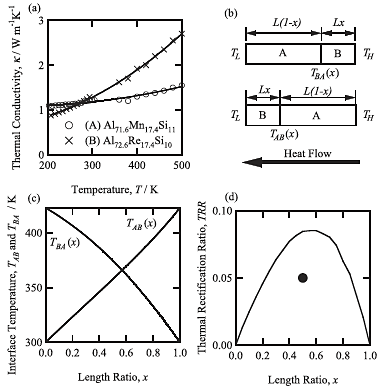
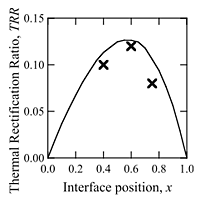
We calculated the length ratio (x = L_AlMnSi/L_AlReSi) dependence of TRR for the thermal rectifier consisting of Al_72.6Re_17.4Si₁₀ and Al_71.6Mn_17.4Si₁₁. The temperature dependence of thermal conductivity, the schematic illustrations of the rectifier, the relation between x and the interface temperatures, and the resulting TRR is shown in Figs. 1(a)-1(d), respectively. The experimentally obtained TRR for x = 0.5 in our previous study is superimposed in Fig. 1(d) with a solid circle. The calculated value for x = 0.5 is TRR = 0.085, and this value is definitely larger than the experimentally obtained value of TRR = 0.05. We considered that this inconsistency between the experiment and the calculation is rather reasonable because T_L in the calculation was assumed to be constant, whereas T_L in the experiment definitely increased with heating time. The increase of T_L naturally leads to a reduction in the difference between (T_L)and (T_H), and consequently to the reduction in TRR.

The consideration described above helped us to understand that the heat current we used in our previous experiment was too large to quantitatively investigate the validity of the method for estimating TRR, and that we should reduce the heat current by reducing the cross-section or extending the length of cylindrical samples. We also realized that the length ratio x = 0.5 that we employed in our previous experiment was not in the best condition, and that the TRR could be increased slightly by using the appropriate length of x = 0.6. We decided, therefore, to perform new experiments in which the heat current density was reduced for proving the validity of the method for estimating TRR. We also employed several samples with varying values of x for increasing the magnitude of TRR of the Al-based thermal rectifier.

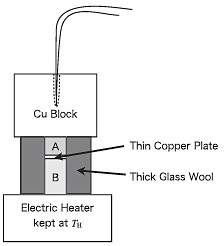
The heat current was estimated by measuring the temperature of a large copper block placed on the composite sample, the bottom of which was heated up using a plate-heater kept at 500K. The experimental setup is schematically drawn in Fig. 2. In order to estimate the heat current flowing through the sample, we assumed that the heat leak from the copper block J_out is simply proportional to the temperature difference between the copper block and the ambient air as J_out = A(T(t)-T_amb). In such a case, the temperature of the copper block increases with heating-time as T(t)=(J_in/A)exp(At/C) +T_amb+(J_in/A). Here C and J_in indicate the heat capacity of copper block and heat current coming through the cylindrical sample, respectively. The magnitude of T_amb + J_in/A was deduced as the saturation temperature T_sat of the transient curve of copper block by fitting it with the equation for the simple relaxation process, T(t)=(T(0)T())exp(t/)+T() . By simultaneously measuring the ambient temperature T_amb, we determined J_AB/A and J_BA/A. Consequently, TRR = (J_AB J_BA)/J_BA was able to be determined even without the information about the magnitude of A.

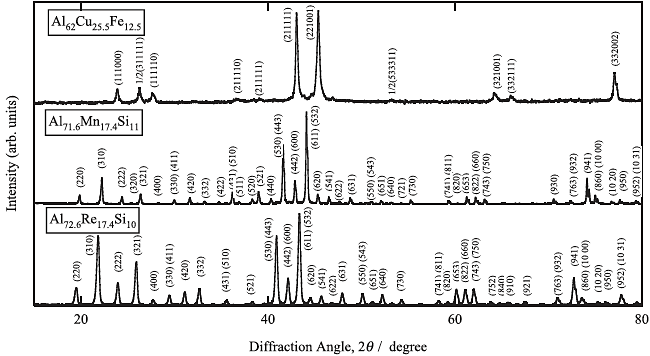
Figure 3 shows XRD patterns of the samples prepared by the induction melting and the subsequent pulsed current sintering process. No evidence of secondary phase precipitation was found in the measured XRD patterns, and the samples were considered to consist solely of the objective phases.

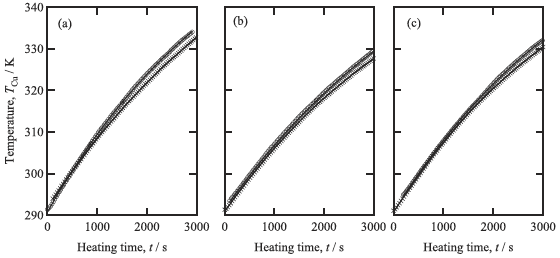
The temperature of the copper block was plotted as a function of heating time in Figs. 4(a)4(c). Obviously, it increases faster when the Al_72.6Re_17.4Si₁₀ was located at the high temperature side due to the larger magnitude of thermal conductivity of Al_72.6Re_17.4Si₁₀ at high temperature. The function fitting with the equation of simplest relaxation process was performed for each transient curve of the copper block's temperature, and the curve obtained by the fitting was superimposed in Figs. 4(a)4(c). The fitted curves coincide with the measured data with negligibly small errors. This experimental fact encouraged us to extract information about the heat current J_AB and J_BA from the measured transient curve of copper block temperature. The reduction of the cross section of the sample must lead to the reduction in the heating rate of the copper block, and indeed, the heating ratio of copper block in this study was definitely reduced from the value obtained from our previous measurement.

The experimentally determined TRR of samples with x = 0.4, 0.6, and 0.75 was plotted in Fig. 5 together with the calculated TRR. The experimentally determined TRR clearly reproduced the calculated TRR, despite that the experimental value was still slightly smaller than the theoretical value mainly due to the small but finite increase of T_L. Notably, the experimentally determined TRR was distributed from 80% to 95% of the theoretically calculated values, and the difference between the experiment and calculation showed a marked decrease from our previous data.

The largest magnitude of TRR obtained in our present experiment was 0.12 at x = 0.6, where the calculated TRR also possesses the maximum magnitude. Although the experimentally obtained TRR = 0.12 is still smaller than the value of TRR~ 0.5 reported for La_0.7Sr_0.3CoO₃/LaCoO₃ at low temperature below 200 K,4 the working temperature of our newly developed rectifier definitely proved the potential of our strategy to develop a practical rectifier usable at temperatures above 300 K.

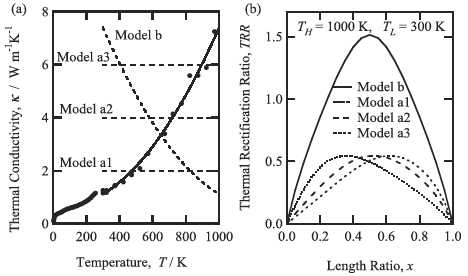
The temperature dependence of the thermal conductivity of the Al₆₂Cu_25.5Fe_12.5 icosahedral quasicrystal is shown in Fig. 6(a). The thermal conductivity of this material possesses at 1000K is almost 7 times greater in magnitude than that at room temperature. This drastic increase in thermal conductivity must produce a large value of TRR when it is coupled with an appropriate material. By employing models for the other component, we estimated the maximum TRR of the thermal rectifier involving the Al₆₂Cu_25.5Fe_12.5 icosahedral quasicrystal as one of the components. One group of the model materials (models a₁-a₃) was assumed to possess a constant thermal conductivity regardless of the temperature as _a(T) = const. The other model material (model b) shows thermal conductivity decreasing with increasing temperature as _b(T) = _Al-Cu-Fe(1300T) at 300 K T 1000 K. The hypothetical thermal conductivities employed in this study are superimposed in Fig. 6(a).

We calculated TRR using the method described in this paper, and the resulting TRR were plotted as a function of x in Fig. 7(b). The calculation clearly predicted that we could potentially obtain values of TRR exceeding 1.5 for the Al₆₂Cu_25.5Fe_12.5 icosahedral quasicrystal, provided that we find the materials possessing the similar thermal conductivity as that of the model b. Since the constant thermal conductivity at high temperature above 300 K is rather easily obtained from many solid materials, it would be also very interesting to note that the magnitude of TRR would exceed 0.5 even if the thermal conductivities of the combined materials were constant.

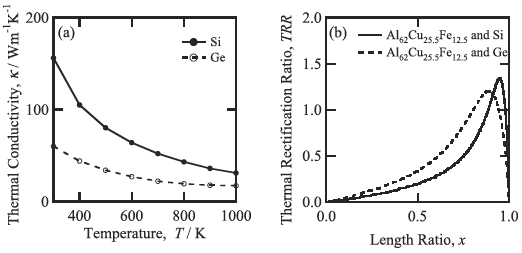
Finally, we show the x dependence of TRR calculated for the thermal rectifiers consisting of Al₆₂Cu_25.5Fe_12.5 icosahedral quasicrystal and a semiconducting, single grained material, Si or Ge, both of which are characterized by a high Debye temperature. TRR was calculated for T_L = 300 K and T_H = 1000 K, and plotted as a function of length ratio x = L_{Si or Ge} / L_Al-Cu-Fe in Fig.7 (b). The large magnitude of TRR exceeding unity was obtained for the sets of real materials, and the maximum value of TRR was 1.34 and 1.24 for Si/Al₆₂Cu_25.5Fe_12.5 and Ge/Al₆₂Cu_25.5Fe_12.5, respectively.